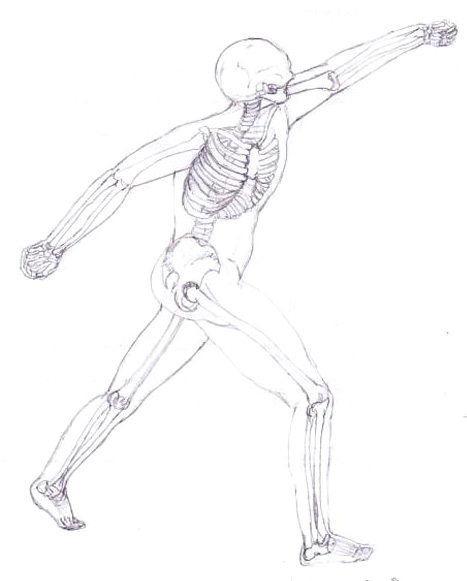
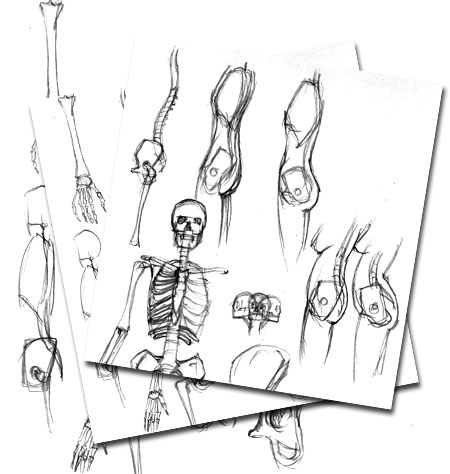
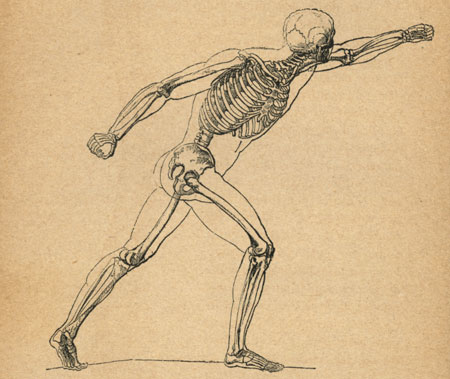
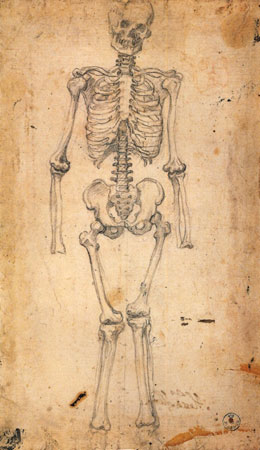
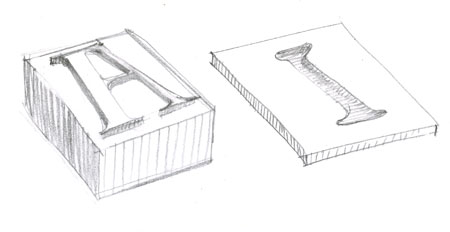
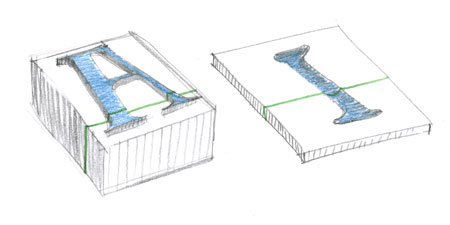
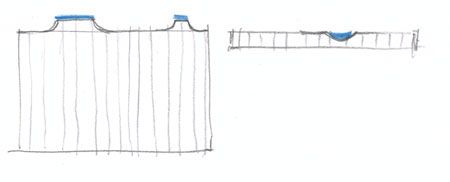
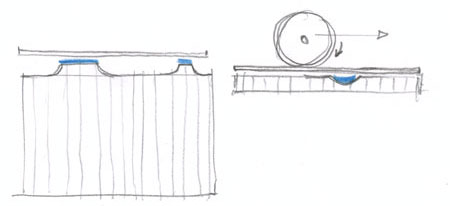
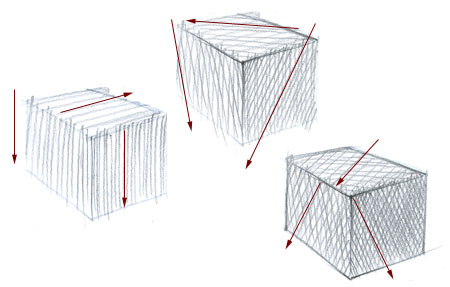
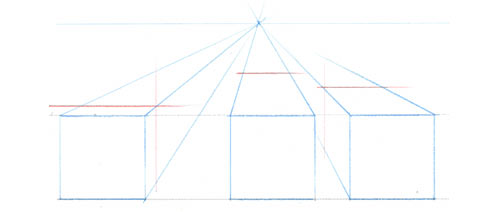
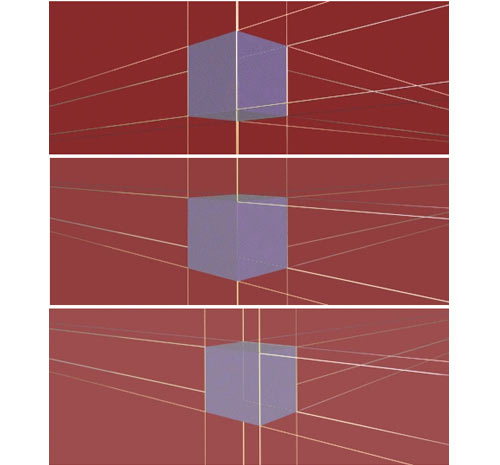
La perspective du cube
Ce qu'il vous faut
Voici le matériel nécessaire pour profiter pleinement de ce module :
Pas de matériel supplémentaire
nécessaire aujourd’hui
L'Observatoire
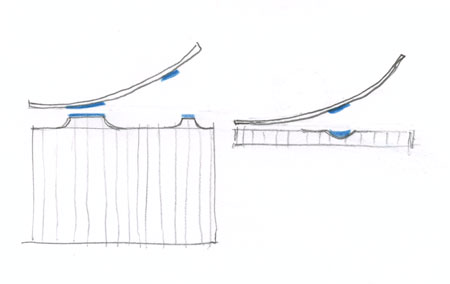
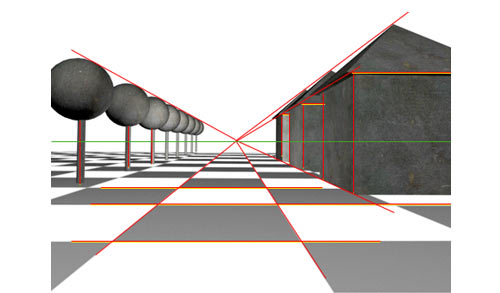
Ce qui est évident ne se voit pas toujours !
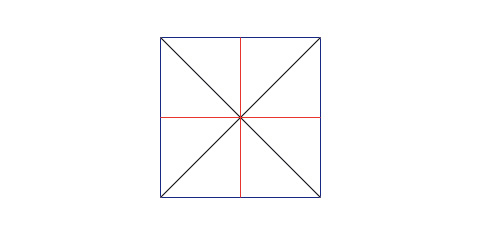
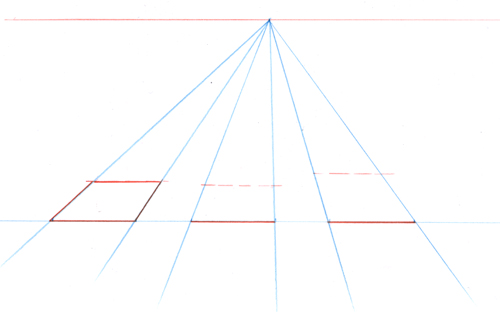
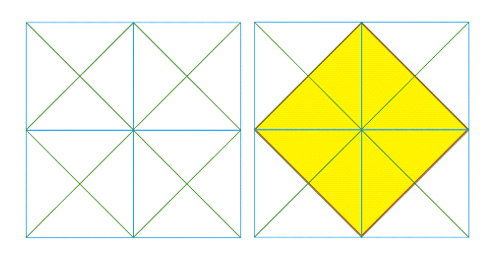
Voici un carré bleu foncé. Ses diagonales sont tracées en noir et ses médiatrices en rouge.
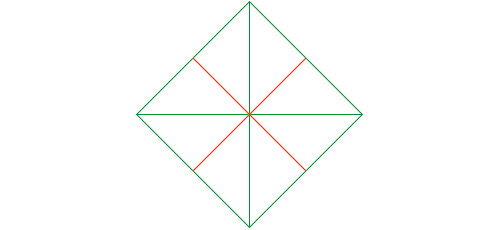 Voici un carré de la même taille mais basculé de 45 °. Les médiatrices sont aussi en rouge.
Voici un carré de la même taille mais basculé de 45 °. Les médiatrices sont aussi en rouge.
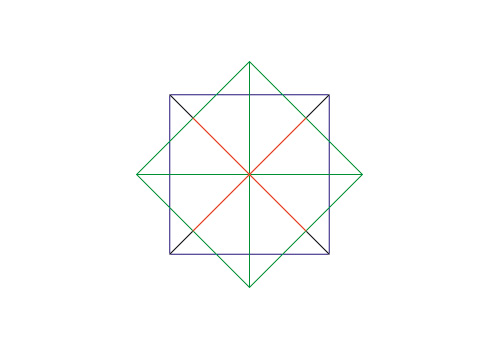
Voici les deux superposés. Les diagonales de l’un se confondent avec les médiatrices de l’autre.
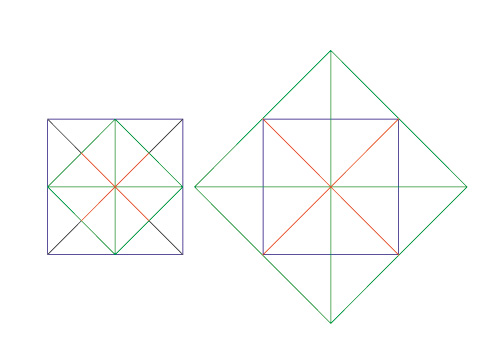
Cela reste vrai quand les deux carrés sont de tailles différentes. Cette simple observation va nous rendre des services incroyables pour dessiner toutes sortes de volumes en perspective. C’est pour cette raison qu’après avoir découvert dans un module précédent comment tracer un carré en perspective, vous allez maintenant en déduire la construction exacte du cube.
Le rideau se lève dans un instant…
Atelier Découverte
Un petit rappel rapide
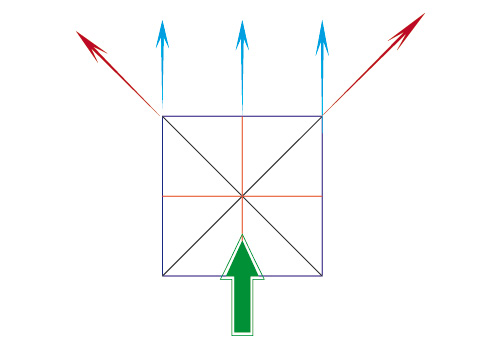
Vue (parallèle) d’un carré en plan
Si vous regardez un carré (ici vu d’en haut) dans la direction qu’indique la flèche verte, c’est que vous êtes en perspective frontale (dite aussi parallèle).
La médiatrice et les côtés parallèles à votre rayon visuel fuient vers le point principal, les diagonales fuient vers les points de fuite des diagonales.
La médiatrice et les côtés perpendiculaires à votre rayon visuel ne fuient pas.
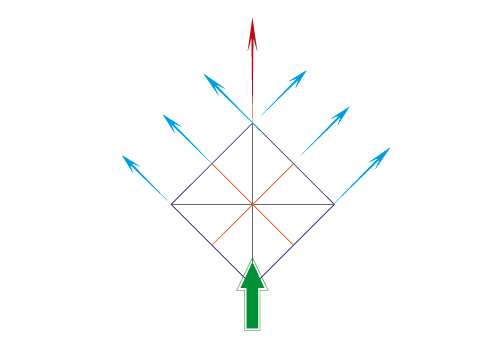
Vue (angulaire) d’un carré en plan
Si le carré subit une rotation de 45 °sur l’axe vertical, vous entrez en perspective angulaire et les fuites s’inversent. Ce sont maintenant les côtés et les médiatrices qui fuient vers les points où convergeaient les diagonales du carré en perspective parallèle. Du même coup, la diagonale qui devient parallèle au rayon visuel fuit vers le point principal et l’autre ne fuit plus du tout, étant perpendiculaire au rayon visuel.
Comment dessiner un cube exact ?
Pour faire un volume parallélépipédique en perspective, il faut commencer par mettre sa base en perspective. Si vous voulez construire un cube exact, la base sera un carré exact.
Or, vous avez appris à dessiner un carré exact. Mais ce carré était en vue parallèle.
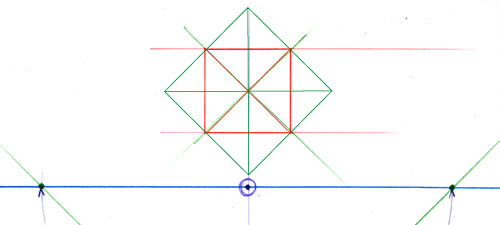
Si le carré était en vue angulaire, comme ce carré vert qui a justement subi une rotation de 45 ° pile, vous pourriez vous débrouiller. En effet, le carré (en rouge) inscrit dans le carré vert étant le même que le précédent, les diagonales et les médiatrices s’intervertissent et la construction est simple à réaliser.
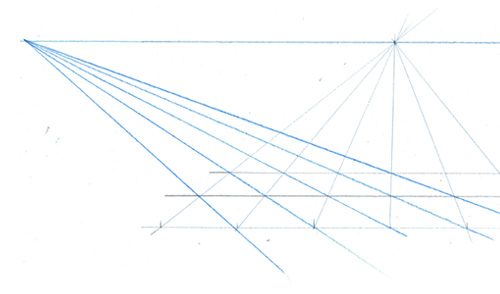
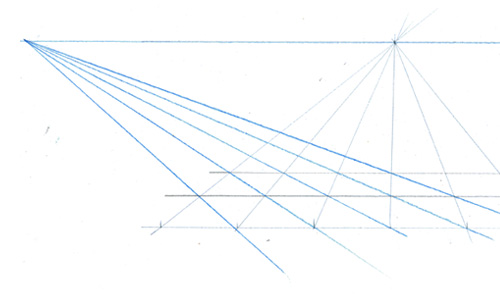
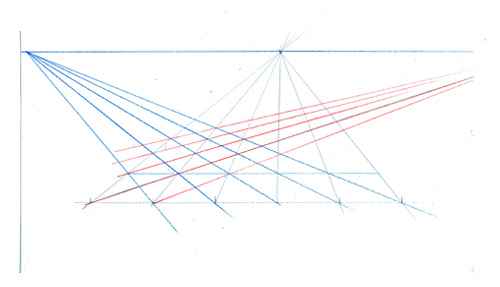
Un réseau de lignes fuyant vers le point principal et vers le point de fuite des diagonales vous permet de vous tirer d’affaire…
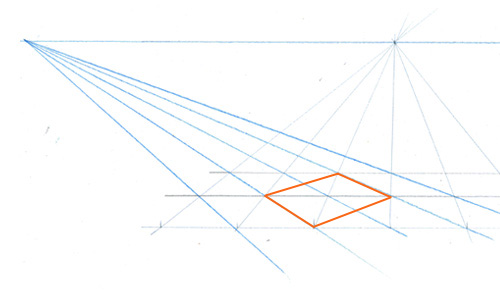
… et de tracer un carré en perspective angulaire si l’une de ses diagonales est parallèle exactement à votre rayon visuel. Mais vous noterez simplement que la taille et la position du carré sont assujetties à la taille de la grille de construction.
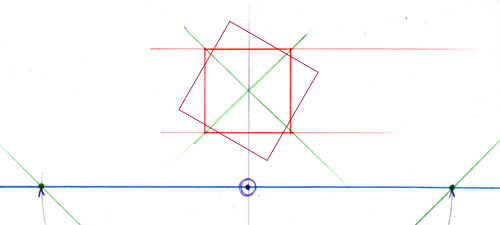
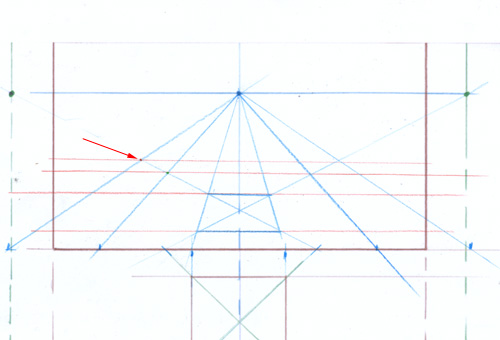
Mais, maintenant…. que faire, si le carré de départ subit une rotation de quelques degrés seulement et que la “grille des diagonales” ne puisse plus vous aider ?
Boîtes, cubes, etc.
Dans votre vie de dessinateur, vous serez amené à dessiner toutes sortes de “boîtes en verre” pour y installer des volumes. Non seulement des volumes primitifs tels que les cônes, les pyramides, les cylindres, mais aussi des volumes beaucoup plus complexes et organiques.

Même pour représenter le corps humain, vous gagnerez énormément de précision en installant vos personnages et vos objets complexes dans des “cages”.
Ces cages font d’excellents guides et sont beaucoup plus faciles à dessiner en racourci que les bras ou les jambes. Elles deviendront de plus en plus légères et finiront, au fur et à mesure que vous progresserez, par être mentales uniquement.
Voilà pourquoi cette étude des volumes cubiques ou des dérivés du cube tient une place aussi importante dans le parcours que je vous propose.
Différents cas de figures
vue en plan
Vous pouvez avoir, au sol, un carré ou un rectangle orienté en long ou en large…
… ou orientés à 45 °
ou de manière plus aléatoire.
Par ailleurs, vous pouvez être placé à droite, en face ou à gauche de ces formes vues en plan.
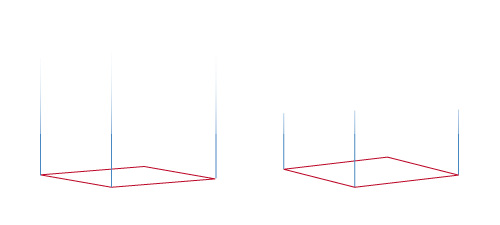
Ensuite, la hauteur de vos boîtes peut varier. Votre propre hauteur également. Si vous réalisez un cube parfait, vous devrez trouver un moyen de calculer la hauteur exacte de ce volume.
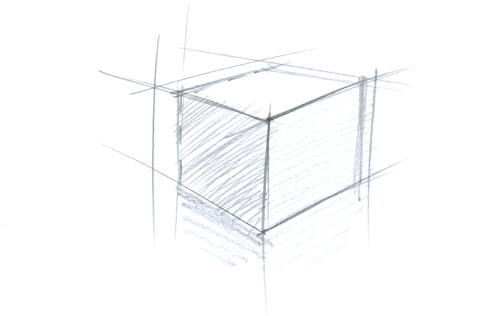
Et si, bien souvent, vous vous contenterez d’avancer à tâtons, il est d’autres cas où une connaissance de la bonne méthode de construction sera indispensable.
Alors, essayez de vous immerger dans cette hypothèse simple en premier lieu.
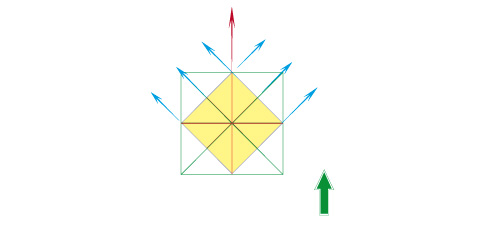
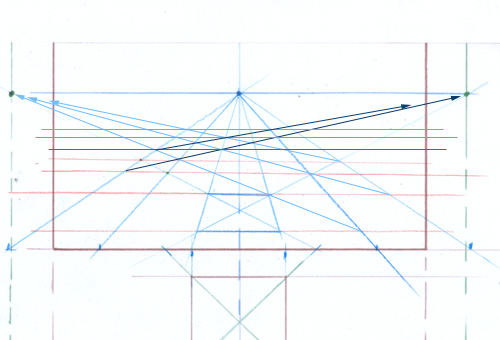
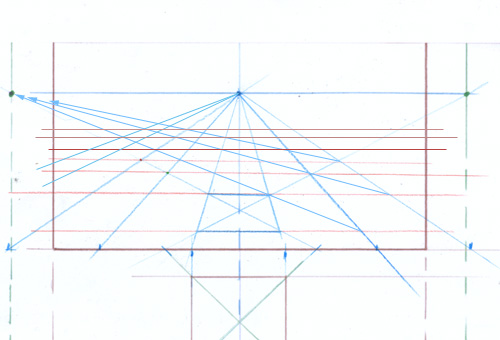
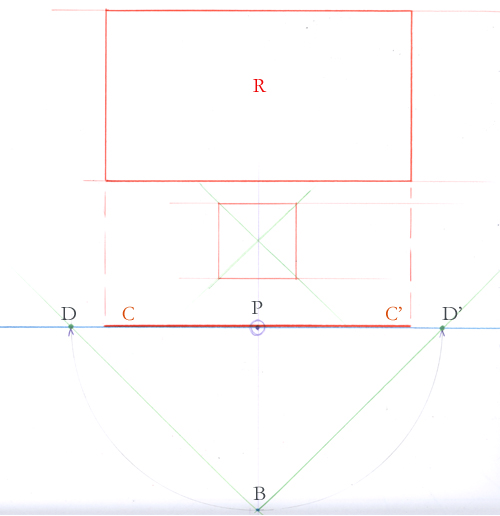
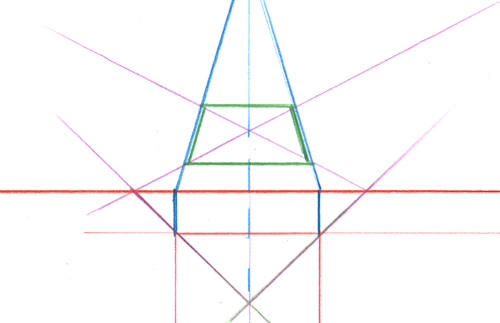
Voici la situation en plan. Vous êtes situé légèrement à droite du carré jaune inscrit dans le carré vert.
Pour mettre cela en perspective, vous tiendrez compte de votre point de vue.
Vous voyez que le carré jaune se présente par un angle, et non par un côté.
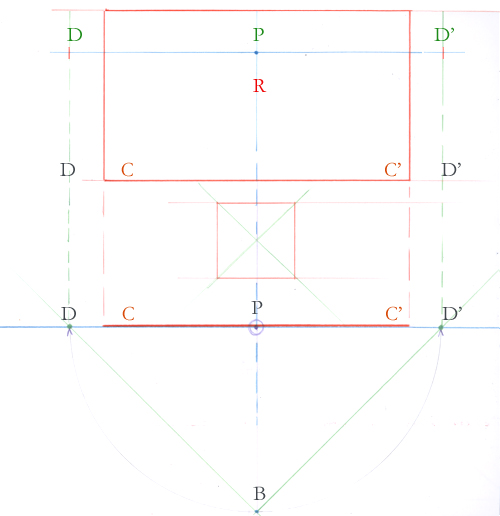
Puisque vous connaissez et que vous pouvez placer au moins l’un des points de fuite des diagonales du carré extérieur, ce sera, du coup, aussi le point de fuite des côtés et des médiatrices du carré jaune.
Si le carré jaune est la base d’un cube que vous voulez dessiner, ce sera également le point de fuite des faces de ce cube.
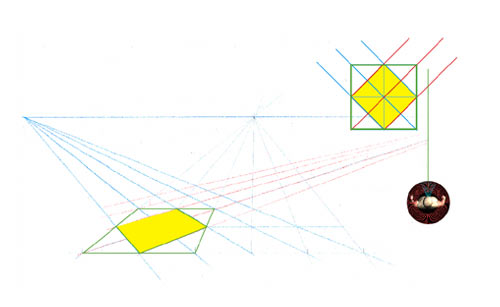
Voici le quadrilatère jaune mis en perspective. Il a suffit de placer sur la grille ses 4 coins, facilement repérables sur la vue en plan. Tout repose ensuite sur la qualité de votre grille et sur son exactitude.
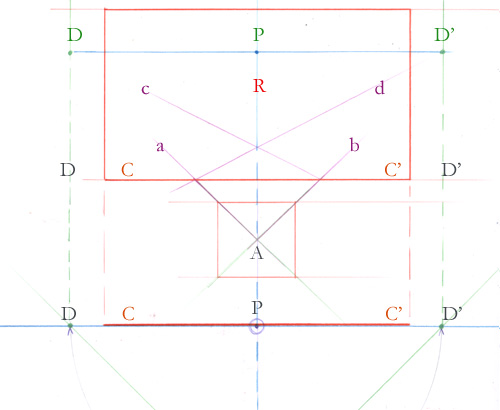
Rien de plus simple que de monter la boîte qui repose sur cette base jaune.
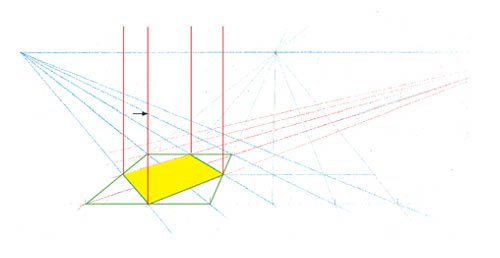
Montez des verticales à partir des quatre coins du carré. Vous matérialisez ainsi les arêtes de la boîte. Choisissez une hauteur à votre convenance sur l’arête la plus proche de vous. La petite flèche noire indique ce choix. Si vous vouliez monter un cube exact, il faudrait pouvoir choisir ce point à une hauteur absolument égale à la longueur d’un côté du carré jaune. J’expliquerai plus tard comment le faire.
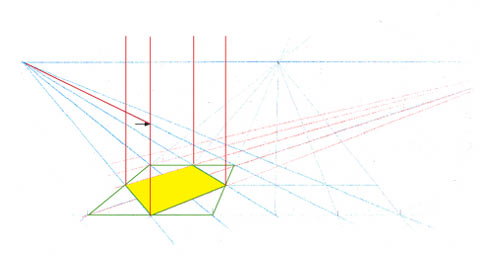
Joignez le point indiqué par la flèche au point de fuite situé sur la ligne d’horizon. Cela vous donne une première face verticale en perspective.
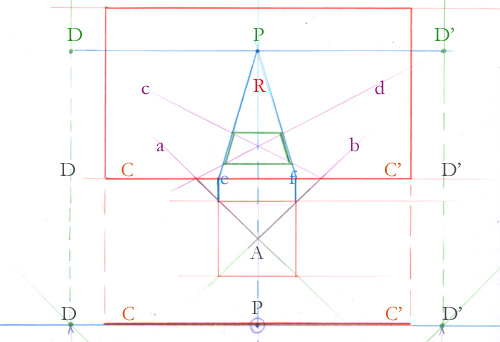
Et maintenant, comment fermer le dessus de la boîte ?
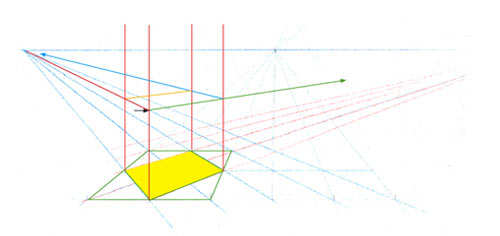
Si vous aviez accès au deuxième point de fuite, vous pourriez placer la ligne verte qui fuirait vers ce point, puis la bleue, et, enfin, fermer le dessus de la boîte avec la ligne orange clair. Comme vous n’avez pas accès à ce point, il va falloir contourner la difficulté. Avez-vous une idée ?
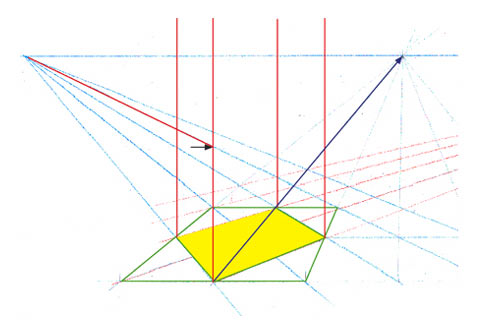
Voici une des nombreuses possibilités : l’une des diagonales du carré jaune ( en bleu foncé) est bien parallèle à votre rayon visuel. Elle fuit donc vers le point principal.
Alors, dans ce cas, on peut tracer la diagonale du couvercle.
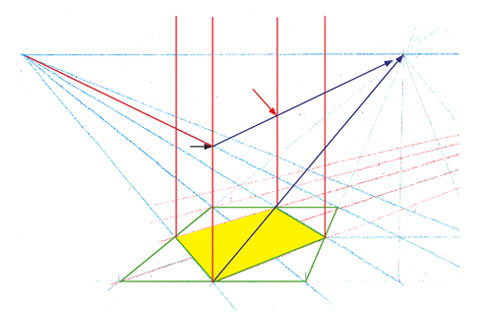
Il suffit de tracer une droite allant du point indiqué par la flèche noire jusqu’au point de fuite principal. Cela reporte la hauteur de la flèche noire sur l’arête située à l’arrière-plan. Ce point est indiqué par la flèche rouge.
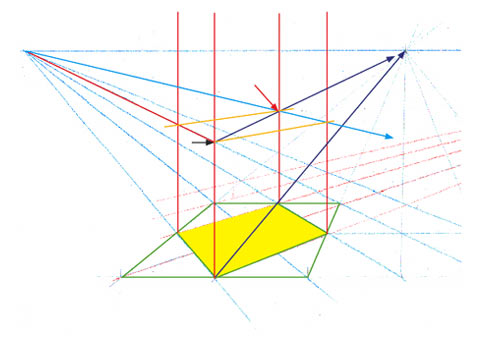
Tracez enfin la ligne bleu clair qui part du point de fuite de gauche et passe par l’angle situé à la flèche rouge. Reliez les coins restants par deux lignes, ici en orange clair, et le dessus de la boîte sera complet. Ces lignes, si elles étaient prolongées fuiraient vers le deuxième point de fuite des diagonales de la grille.
La problématique du cube

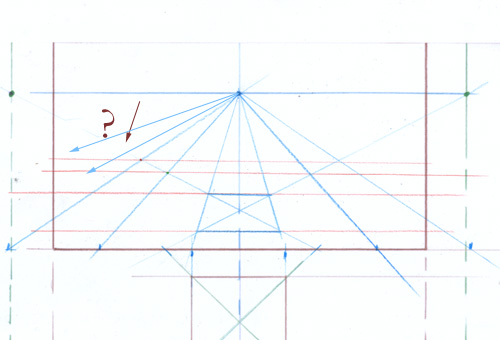
Vous avez vu, il y a quelques instants, que la flèche noire avait été placée à une hauteur arbitraire. Pour la placer avec précision dans le but de tracer un cube, nous avons des moyens variés. Quelle serait la méthode la plus simple dans le cas présent ?

Ici, je ne vous demande pas de deviner une règle de perspective, mais seulement de réfléchir à ce que vous avez à votre disposition pour résoudre le problème. Réfléchissez-y, puis regardez plus bas.
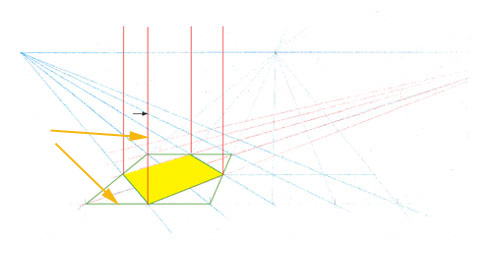
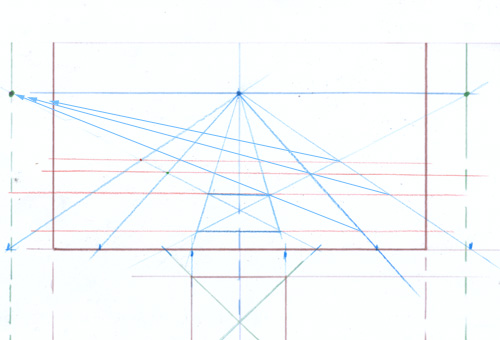
Vous voyez que les deux lignes pointées par des flèches sont sur un même plan vertical. Elles sont à égale distance de votre oeil. Vous pouvez donc les comparer.
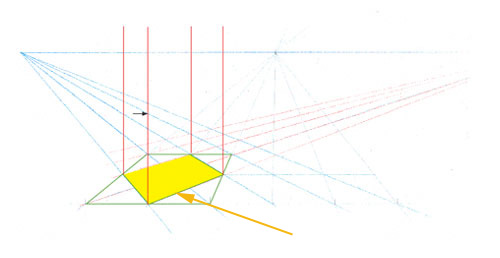
Cela veut dire que, s’il était possible de “relever” le côté du carré jaune sur la ligne rouge, tout serait réglé. Or la chose est possible en 2 mouvements :
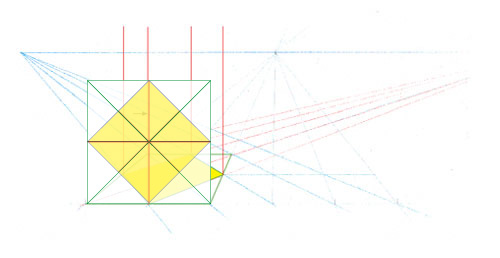
1- relever le dessin verticalement sur une charnière imaginaire située sur le côté avant du carré.
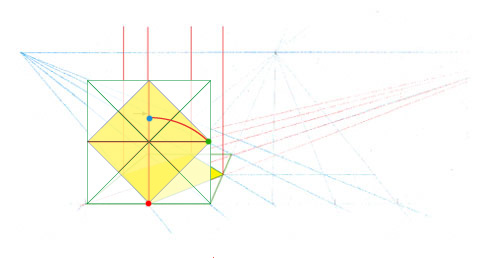
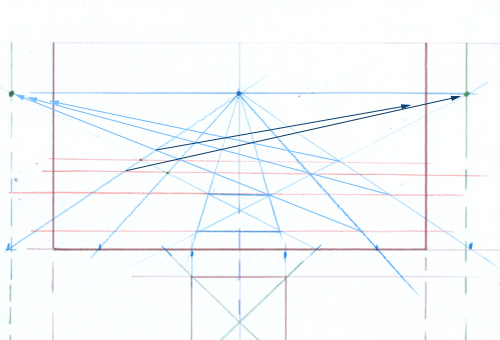
2- placer la pointe d’un compas au point rouge pour reporter le côté du carré sur la verticale. La distance du point rouge au point vert est forcément égale à celle du point rouge au point bleu.
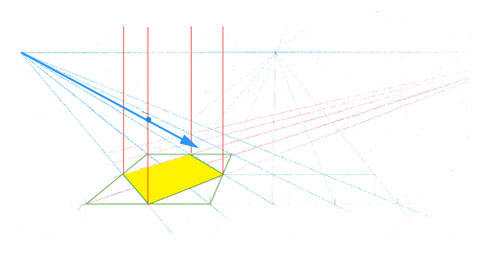
La suite se déroule de la même manière que dans l’exemple précédent. Une fuyante est tracée à la hauteur de ce point…
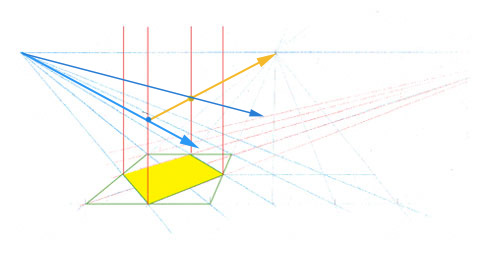
Puis la diagonale de la face supérieure qui fuit au point principal, et le reste en découle naturellement.
Découvrez maintenant en vidéo comment monter un cube, bien cubique, avec très peu de moyens.
C’est dans l’Atelier Pratique.
Atelier Pratique
Construire un cube en perspective angulaire
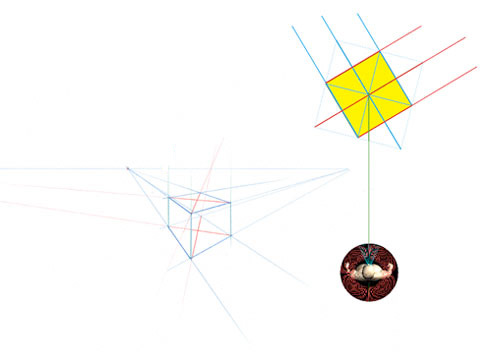
Le cas précédent était un peu trop idéal ; le carré se présentait à vous par un angle de 45° exactement.
Il peut se trouver que le carré se présente par un angle différent. Dans ce cas, ses diagonales ne sont pas perpendiculaire pour l’une, ni parallèle pour l’autre, à votre rayon visuel.
Du coup, les points de fuite ne sont pas à égale distance du point principal. L’un est beaucoup plus près de ce point que l’autre.
De même les lignes diagonales, en rouge sur le cube en perspective, convergent vers leurs points de fuite respectifs à des distances très inégales du point principal. Celui de gauche sort même de la feuille.
Il ne faut pas vous laisser impressionner par cela. La construction reste la même.
Voyez maintenant cette vidéo
La technique de perspective montrée dans cette vidéo fera l’objet d’une explication complète dans les modules suivants de cette branche. Contentez-vous pour l’instant de constater que cette méthode existe et refaites éventuellement cet exercice pour vous-même, étape par étape.
Il ne vous reste pratiquement plus qu’à creuser un peu la perspective aérienne et vous aurez entre les mains pratiquement tout ce qui est nécessaire pour dessiner un volume, quel que soit le point de vue choisi.
La perspective aérienne peut se justifier en vue frontale comme en vue angulaire. Elle repose sur l’ajout d’un point de fuite supplémentaire. Au total, vous aurez deux points de fuite au lieu d’un en vue frontale et trois au lieu de deux en vue angulaire.
Regardez ce quadrilatère vu en perspective angulaire. Imaginez, qu’au lieu d’une dalle, ce rectangle mis en perspective soit le toit d’un immeuble, ou même celui d’un gratte-ciel dont vous vous approcheriez en hélicoptère. Pour vous prouver que la perspective aérienne n’est pas difficile, cet exemple part d’une vue angulaire avec justement des points de fuite non équidistants du point principal.
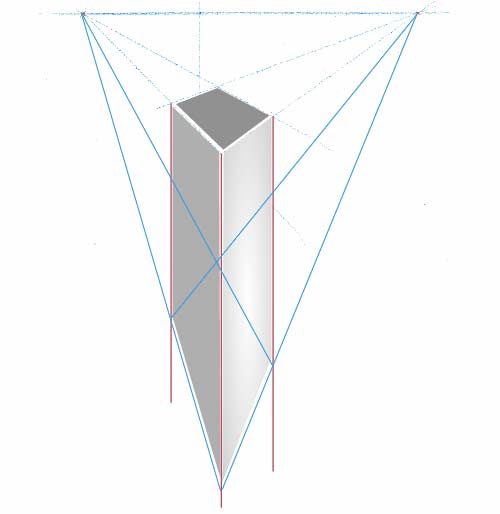
Voilà ce que donnerait l’application de la perspective angulaire telle que vous la connaissez.
Vous sentez bien que cet immeuble a l’air bancal. On dirait même qu’il est plus large à sa base qu’en haut. C’est faux, mais votre oeil vous trompe. Le coin de ce bâtiment a l’air aussi d’avoir un angle obtu en bas. Il a l’air déformé par un objectif grand angle.
Il y a une bonne raison à cela. Vous savez maintenant ce qu’est la dégradation linéaire. Le carré qui forme la base de l’immeuble est très éloigné de la terrasse.
Il devrait donc être plus petit, or il est plus grand.
Pour remettre tout ceci d’aplomb, il faut ajouter un point de fuite.
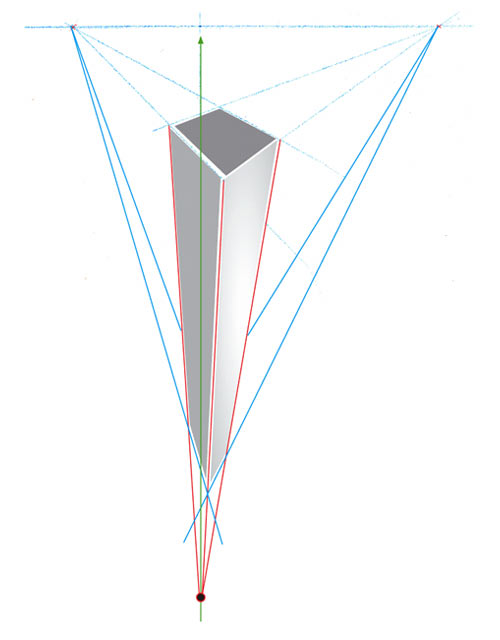
Vous allez placer ce point de fuite sur la ligne verticale, ici en vert, qui passe par le point principal.
Les verticales vont fuir vers ce point.
Son aspect encore curieux lui vient uniquement du choix des deux points de fuite sur l’horizon. Ils sont trop rapprochés.
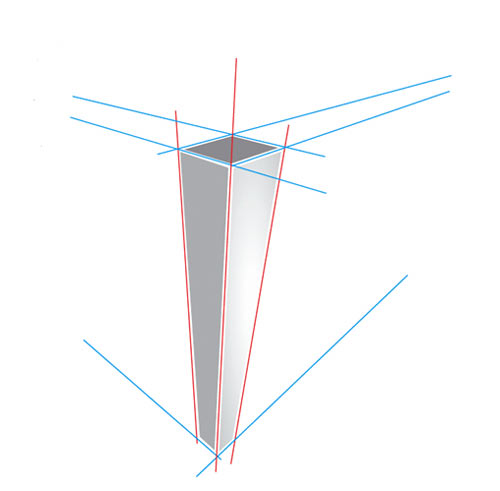
Ecartez les points de fuite pour corriger la construction. Cette fois, l’immeuble semble vu de haut et se déforme de façon acceptable.
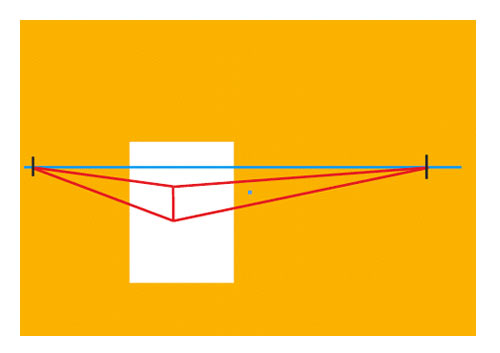
Voilà pourquoi vous serez parfois amené à travailler sur des points de fuite placés hors de la feuille de papier. Si une installation des points de fuite à l’extérieur de votre feuille est impossible, il reste une solution. Découvrez-la dans l’onglet Astuce utile.
Solution
En comprenant le problème, vous trouverez la solution

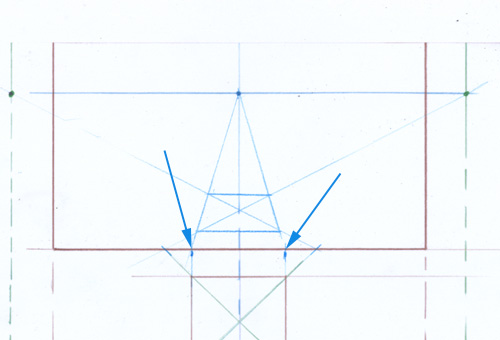
Pour pouvoir dessiner un cube en perspective exacte, il est indispensable que la grille de départ soit parfaitement juste. Ici, rien ne prouve qu’elle soit composée de carrés. Le dallage ne doit pas seulement avoir l’air carré, il doit être dessiné juste.
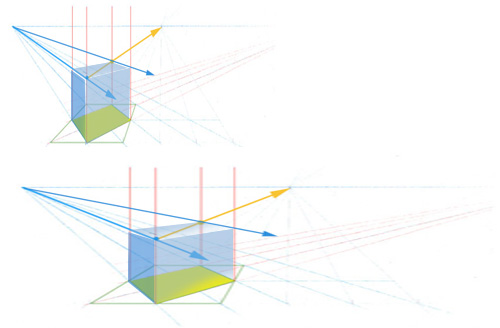
L’écartement des points de fuite joue également un rôle important. Cette image montre le même dessin uniquement étiré pour écarter les points de fuite. Le parallélépipède se transforme complètement.
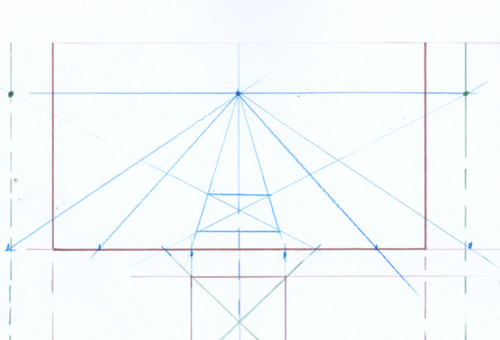
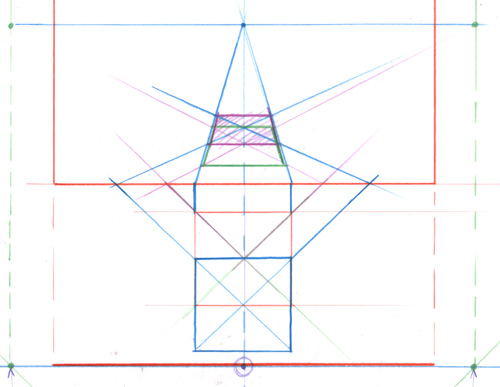
Voici à nouveau le moyen classique et pas trop complexe de construire le cube. C’est exactement la méthode de la vidéo mais montée à la règle et à l’équerre.

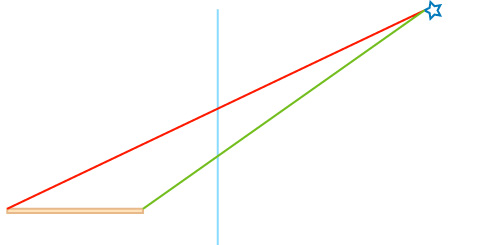
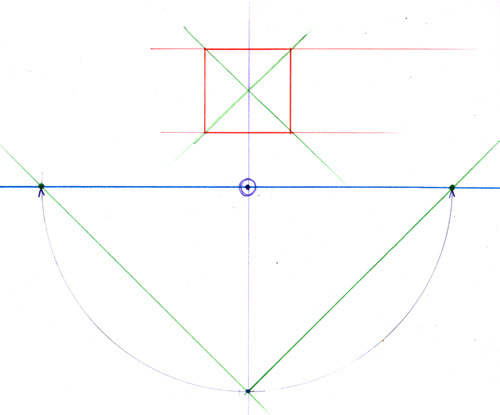
Tracez votre carré vu en plan, posez le sur une ligne de base.

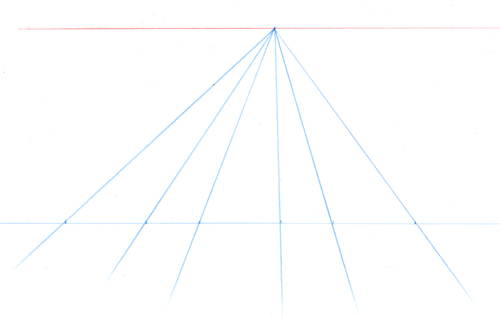
Placez une perpendiculaire à la ligne de base et un point dessus donnant la position du spectateur.

Tracez des parallèles aux côtés du carré partant du point de vue
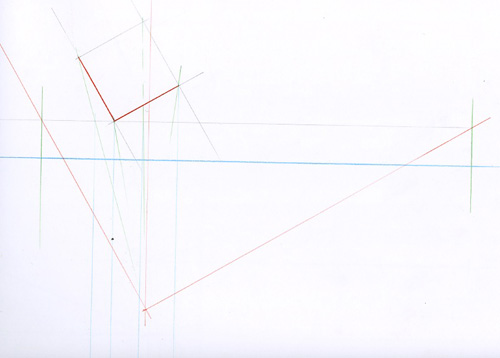
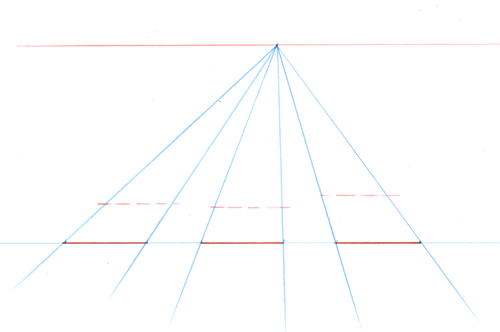
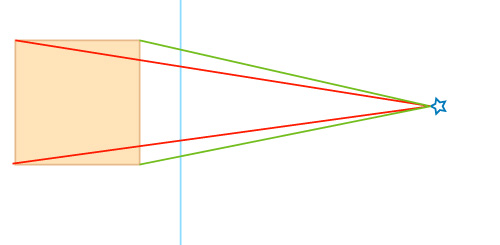
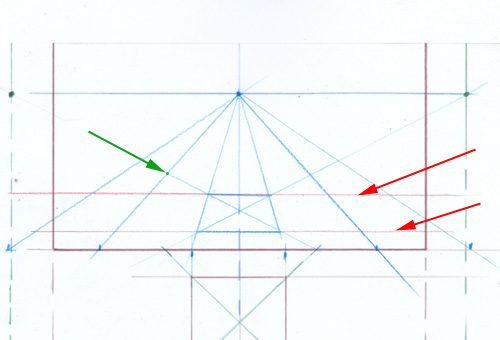
Définissez au choix une ligne d’horizon et abaissez sur elle les points de rencontre de la ligne de base et des deux lignes rouges que vous venez de tracer.
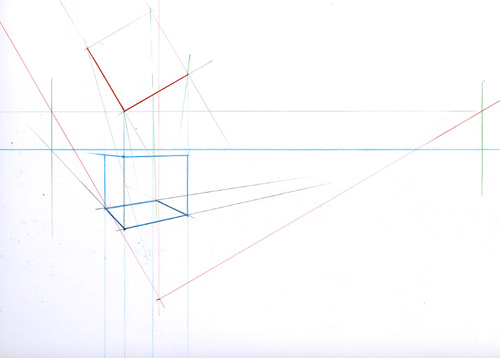
Construisez le cube en utilisant ces nouveaux points comme des points de fuite
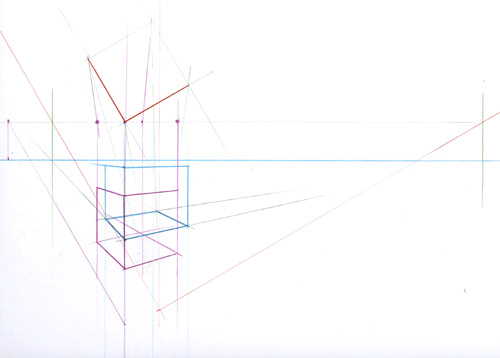
Vous pouvez déplacer le point de vue et refaire la construction. Ici, en violet le point de vue a été placé exactement devant l’arête du cube la plus proche de nous.
Ne vous inquiétez pas si tous ces tracés vous semblent un peu difficiles. Il n’est pas question de les retenir. Trempez-y un orteil de temps en temps et vous verrez que vous allez y prendre goût.
Nous y reviendrons et à chaque fois cela vous semblera plus évident. On entre pas du jour au lendemain dans la troisième dimension.
Astuce Utile
Comment faire lorsque les points de fuite sont en dehors de la feuille

Une première solution consiste à placer votre feuille sur une surface assez grande, comme une planche à dessin, pour pouvoir placer les points de fuite en y plantant une épingle, par exemple.
Mais il se présentera toujours un cas où votre planche sera trop petite et où les points de fuite devraient être placés à plusieurs mètres du point principal. Vous utiliserez alors une autre méthode que voici :

Imaginez ceci : vous voulez mettre en place, assez précisément, un volume parallélépipédique en vue angulaire, un bâtiment par exemple. Ceci dit, l’échelle ne compte pas. Le volume pourrait être un immeuble ou une boîte d’allumettes, le principe reste le même.
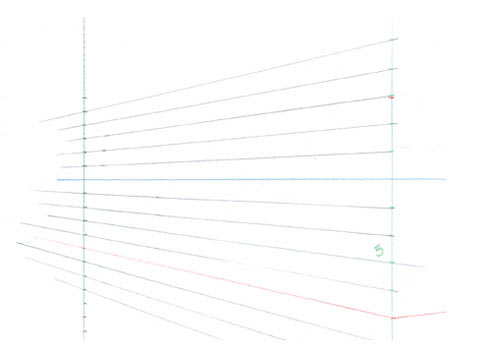
Tracez votre ligne d’horizon, puis une verticale que vous placez où vous voulez.
Cette verticale matérialisera l’arête verticale la plus proche de vous.

A partir de cette verticale, tracez deux fuyantes (ici en rouge), dont l’aboutissement sera en dehors de votre feuille. Les deux points de fuite de cette vue angulaire n’ont pas besoin d’être équidistants de la verticale. Les angles seront donc éventuellement différents mais les angles que font ces fuyantes avec la verticale seront assez ouverts pour que les points de fuite soient bien éloignés. Ainsi, la déformation désagréable, qui arrive lorsque deux points de fuite sont trop rapprochés, ne risque plus de se produire.
Marquez maintenant d’un point une hauteur quelconque sur la verticale. Vous voyez bien que vous ne pouvez pas relier ce nouveau point aux points de fuite, puisqu’ils sont inaccessibles.
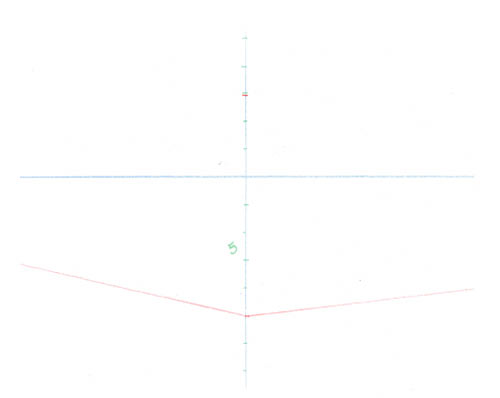
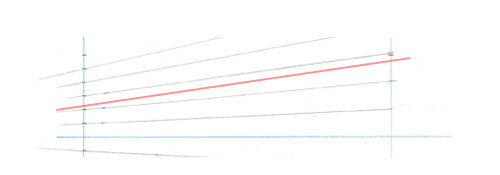
Mesurez la hauteur entre l’angle inférieur et l’horizon sur la ligne verticale. Divisez-la par un nombre quelconque et tracez les divisions. Arrangez-vous pour que les calculs soient simples. Ici, la hauteur étant juste de 5 cm, vous prenez naturellement cinq divisions de 1 cm chacune.
Si vous n’avez pas de chance, pliez une petite bande de papier en deux puis en 4 et utilisez ces plis comme divisions.
Ajoutez encore des divisions semblables au-dessus de l’horizon et en-dessous du “coin” inférieur.
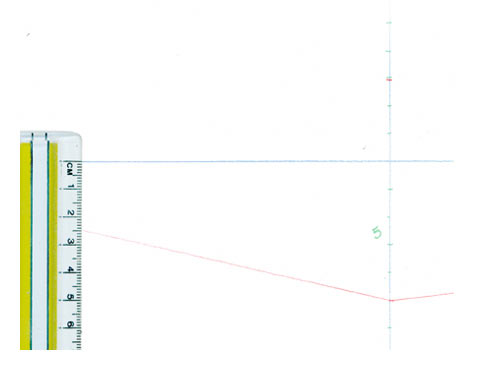
Cherchez maintenant, avec une règle graduée placée bien verticalement, l’endroit où tracer facilement le même nombre de divisions utilisant un sous-multiple des précédentes. Ici, vous pouvez chercher le point où la hauteur entre l’horizon et la fuyante de gauche mesure 25mm. Cela correspond à 5 divisions de 5mm.

Tracez vos divisions de 5mm de part et d’autre de l’horizon, en dépassant encore une fois en haut et en bas.
La même opération à droite serait impossible, puisqu’au bord de la feuille elles sont encore espacées de plus de 25mm. Tracez, dans ce cas, une verticale plus près du centre qui soit un multiple de 5. Exemple : 5 fois 7mm. Ceci vous ferait chercher la position d’une verticale faisant 35mm entre les deux lignes.
Reliez maintenant vos divisions et vous disposez d’une grille pour vous guider.
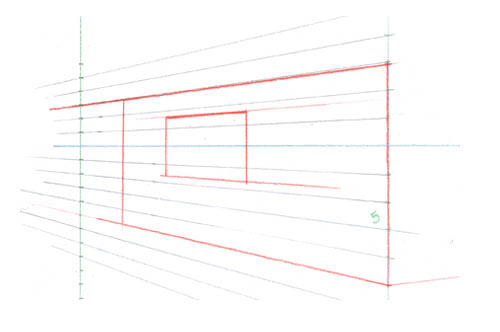
Vous n’aurez plus besoin du point de fuite; il suffira de placer vos fuyantes à l’oeil entre deux lignes de la grille. Plus la grille sera serrée, plus votre tracé sera exact.
Si, comme dans cet exemple à ne pas imiter, la ligne que vous tracez est mal orientée, elle semblera ne pas suivre le réseau de lignes que constitue la grille. Votre oeil s’en apercevra aussitôt.
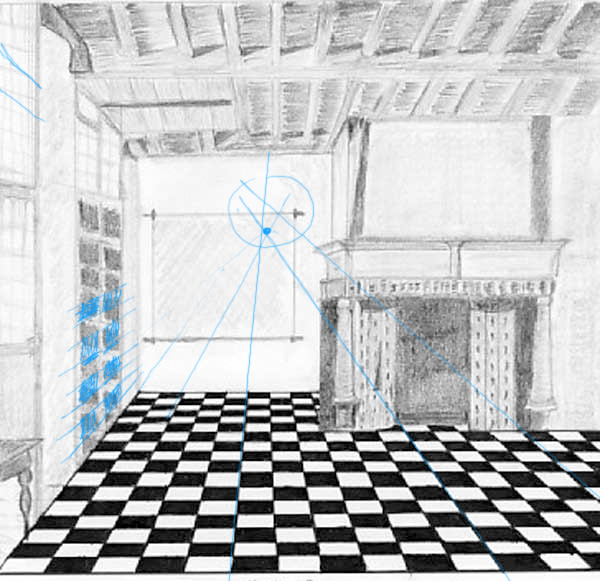
Très utile pour dessiner les intérieurs meublés, cette technique est à retenir pour sa grande précision pourtant purement visuelle.
Dessins à Faire
![]()
A vos crayons !
Vous trouverez toujours des dessins à faire ou des exercices à votre disposition dans cette rubrique. Les modèles sont aussi des documents qui vous permettent des expériences supplémentaires.
Vous pouvez uploader votre dessin dans les galeries. Vos dessins seront vus par les autres membres et les tuteurs qui pourront, dans certains cas publier une correction s’ils jugent qu’elle peut être utile à tous. Mais cela n’est pas systématique.
Dessins à Faire et à conserver ou publier
DAF-067-1
Réalisez une composition de cubes (au moins 3) sur un format de votre choix. Encadrez la composition d’un filet qui permette de mieux voir l’agencement des cubes dans la surface retenue. Utilisez la méthode et la technique que vous voulez. Vous serez jugé sur les bonnes proportions de vos cubes, sur l’agrément de la composition.
DAF-067-2
Créez un dessin sur le thème du cube parfait, totalement issu de votre propre inspiration, et dont vous soignerez l’exécution.
Dessins facultatifs à conserver
FAC-067-1
Dessinez en perspective angulaire un cube dont une diagonale est parallèle à votre rayon visuel.
Dessinez juste à côté le même cube à main levée, sans aucun tracé préalable. Si cela vous semble trop difficile, faites le FAC-067-2. Si cela vous semble trop simple, passez au FAC-067-3
FAC-067-2
Faites le même exercice mais avec un cube en perspective parallèle.
FAC-067-3
Dessinez un cube en perspective aérienne. Redessinez-le juste à côté à main levée sans aucun tracé préalable. Corrigez éventuellement les excès optiques dus à la perspective. Votre cube doit paraître parfaitement cubique.
Bonus
Voici un article paru dans le magazine Mécanique Populaire en mars 1963.

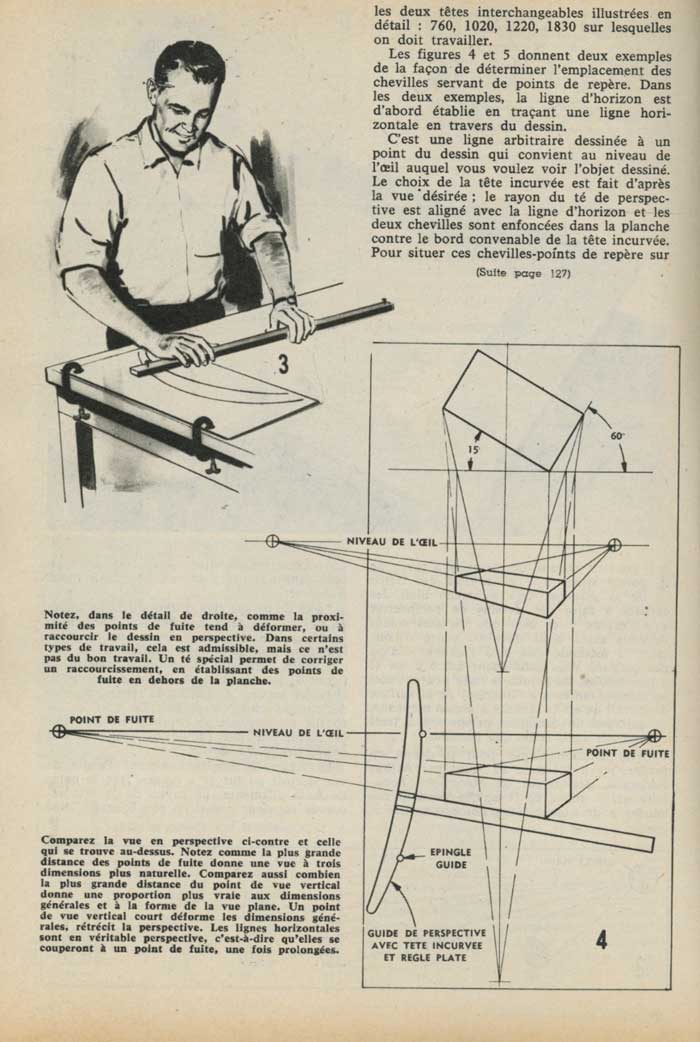
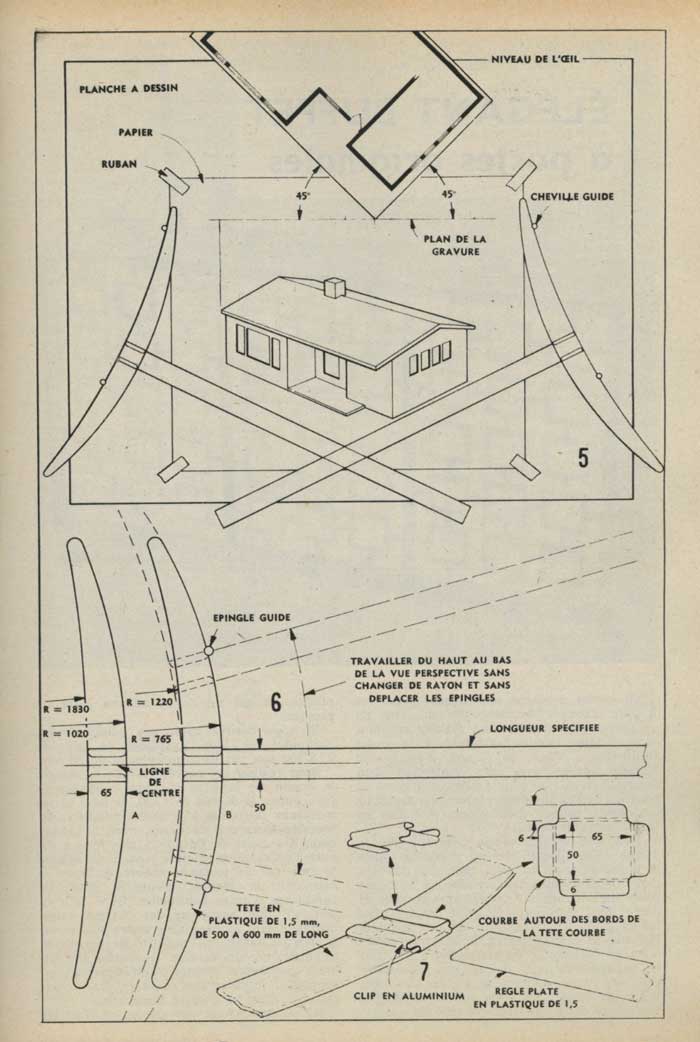

© Mécanique Populaire Tous droits réservés.
Prochainement
Votre prochain module
Objet d’après nature ? Objet de mémoire ?
Est-ce vraiment différent ?

Vous essayerez dans ce module d’acquérir les procédés qui vous donneront envie de prendre un vrai modèle plutôt qu’une photo toute prête.
Matériel à prévoir
Voyez dans cette rubrique le matériel dont vous aurez besoin prochainement.
Ceci vous permet de vous organiser.
 Pas de nouveau matériel
Pas de nouveau matériel
à prévoir dans les prochains jours…
Pour l’instant le matériel déjà en votre possession est suffisant pour les prochains modules. Veillez simplement à le renouveler et le garder en bon état. Vous serez prévenus dès qu’il faudra vous équiper de matériel supplémentaire mais vous aurez largement le temps de vous le procurer.
Correction
![]()
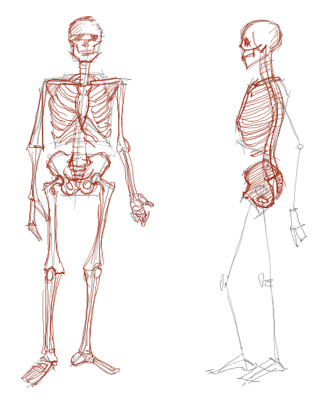
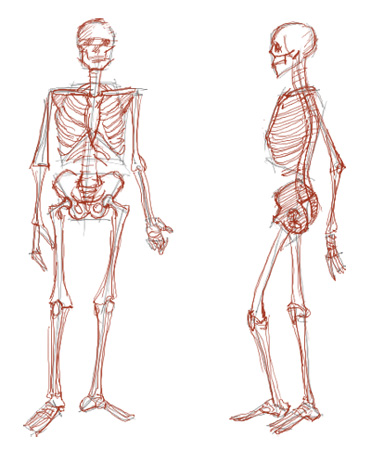
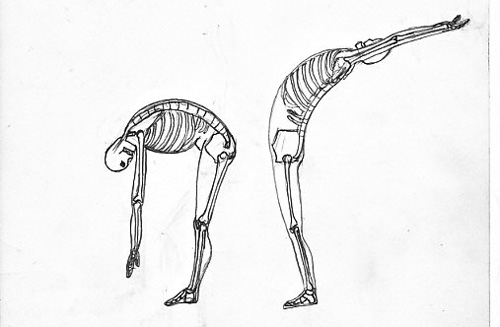
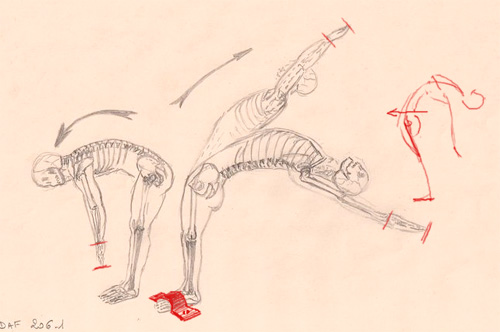
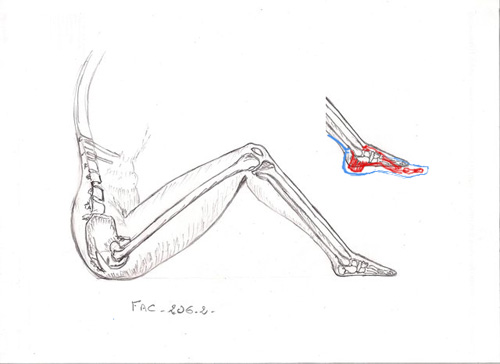
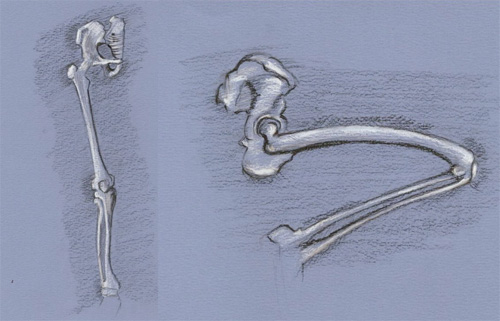
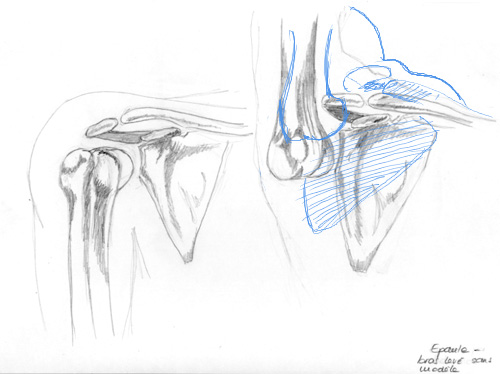
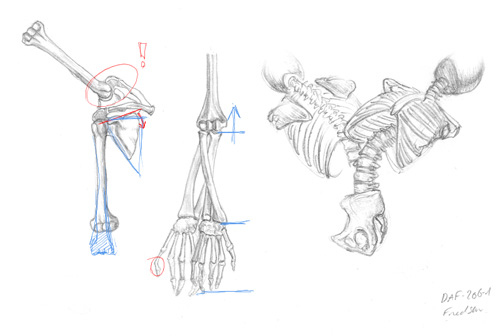
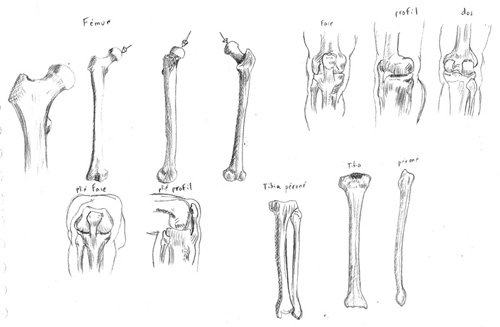
Correction générique du DAF-206-1
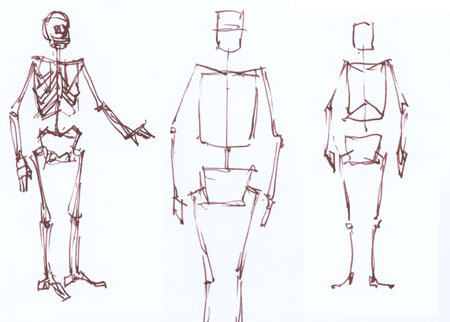
“Encore des os”
Il est plus intéressant que les corrections soient visibles après que vous ayez eu le temps de finir votre DAF. Voilà pourquoi vous trouvez ici la correction d’un DAF antérieur.
Un bon dessin, simple et assez juste…
Conservez un double de vos images chez vous, c’est plus sûr !
Ne mettez ici que les images de vos DAF ou de vos FAC
Vous devez être connecté pour soumettre une image pour le concours. Connexion ouinscrivez-vous.
Conservez un double de vos images chez vous, c’est plus sûr !
Ne mettez ici que les dessins destinés à la Galerie des Membres.
Vous devez être connecté pour soumettre une image pour le concours. Connexion ouinscrivez-vous.
En principe vous trouvez ici tous vos dessins mis en galeries ou en attente de validation.
Il sont aussi accessibles dans une galerie plus confortable dans votre menu Espace Membre/Ma Galerie Perso
Veuillez vous connecter pour voir vos images personnelles
Notez votre progression dans ce module
- Module parcouru rapidement
- Module vu en totalité
- DAF faits
- FAC faits
- Module à revoir
- Module bien assimilé
Vous pouvez changer vos choix à tout moment.
Une fois le module bien assimilé vous pourrez aller noter votre avancement ici